根据知乎用户@heaven的系列博客整理(https://www.zhihu.com/people/yu-xin-hang-22/posts?page=4)
目录
[toc]
1.1 什么是强化学习
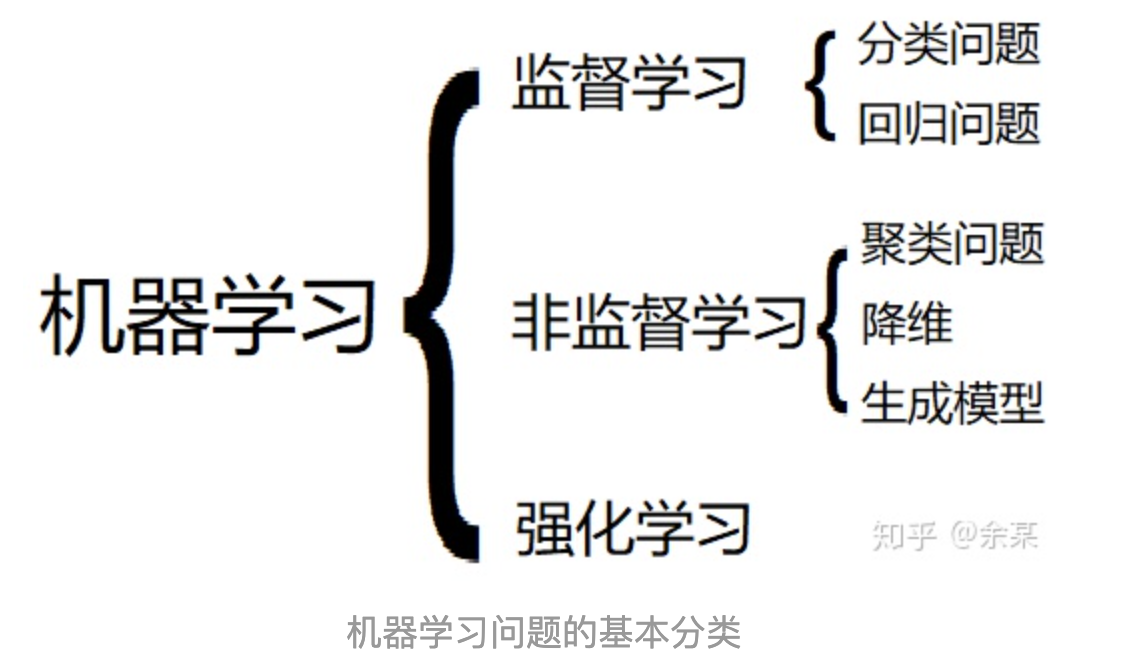
强化学习主要是属于机器学习范畴的一类问题,通常会为这类问题定义以下几个元素:
- 智能体 Agent
- 环境 Environment
- 动作 Action
- 状态 State
-
奖励 Reward
这些元素之间的关系可以由下图表示:
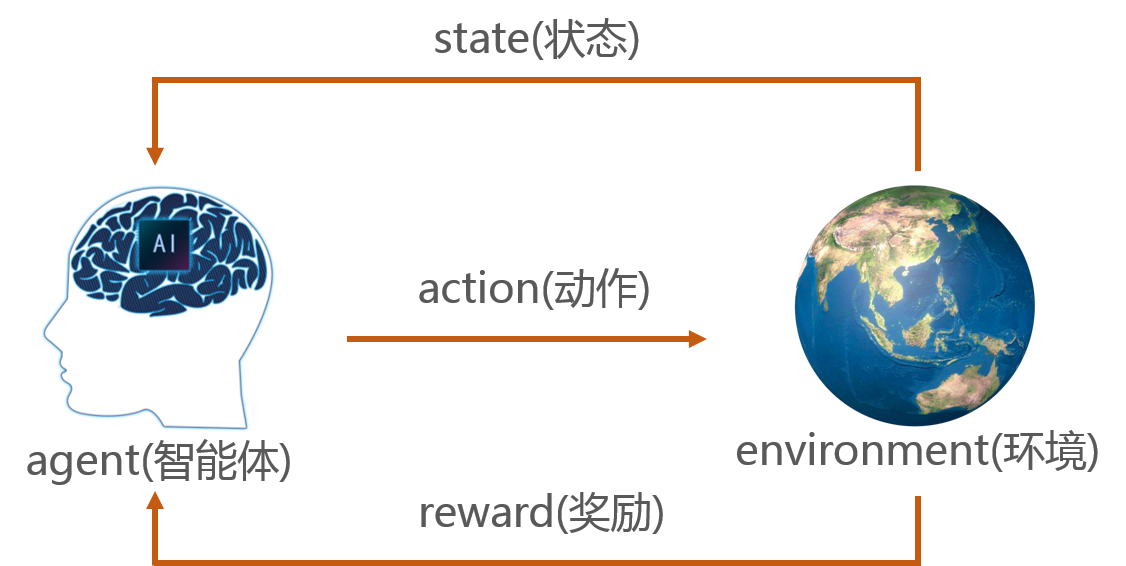
最终的目的是训练智能体选取合适的策略来最大化奖励,策略即面对状态该如何采取动作。
需要注意的是: 当我们提起“强化学习”的时候,往往会用到“深度学习”的方法,并将其称作“深度强化学习”。 但我们要注意不要混淆二者的含义,要清楚“强化学习”是一类问题,而“深度学习”是一类方法。
1.2 强化学习的基本思想
有监督学习和无监督学习:基于已有的数据,去学习数据的分布或蕴含的其他重要信息。 强化学习:不是基于已有数据,而是对一个环境进行学习;且目标不是数据中的信息,而是寻找能在环境中取得更多奖励的方法。
- 监督学习的目标——“弄清楚环境是什么样的”
- 强化学习的目标——“在这个环境中生活得更好”
强化学习算法主要涉及到两个组成部分:其一是通过与环境交互产生大量的数据, 其二是利用这些数据去求解最佳策略
设计强化学习算法时要考虑:计算量;数据效率(产生数据所需的成本);训练效率(求解最优策略的效率)
(1)从环境中产生数据
监督学习—— “拥有数据”意味着拥有环境中随机产生的数据。 强化学习——“拥有环境”意味着可以自主选择与环境交互的方式,从环境中产生我们需要的数据,比随机产生的训练数据包含更多的价值 使探索利用平衡发挥作用
越学越强(强化学习): 对智能体进行初步训练—》有了初步的分辨能力之后—》判断并产生相对更加“重要”的数据 然后用这些数据优化自身的策略—》更准确地判断哪些数据更加“重要”—》更有针对性地从环境中产生更加有价值的数据, 进一步优化自身的策略
强化学习的目标是寻找能够在环境中取得较多奖励的策略。如果仅仅依靠给定的数据是难以求解出很好的策略的。只有拥有可交互的环境,才能充分验证我们策略的有效性。
模仿学习(imitation learning):将强化学习问题转换为有监督学习问题。但实际应用效果很差。 原因——有监督学习目标为优化预测值和真实值的误差。强化学习中,假设训练出来的模型有误差,会导致实际采取的动作有误差,使得下一状态状态也有误差,不断累积,智能体根本无法应对。类似蝴蝶效应 解决方案——DAgger(Dataset Aggregation)。用已经产生的数据进行模仿,对新产生的数据不断进行标注。

Note: 拥有环境 VS 拥有数据。前者更好。 但实践中,缺乏可自由交互的环境,只能通过历史数据学习策略,并用于环境中——Offline Reinforcement Learning (或称为batch RL),
(2)求解最佳策略
- 基于价值(时间查分的思想,即time difference,TD)
- 基于策略(具有优化思想)
最优控制(optimal control)问题:求解一个环境已知的MDP 已知环境表达式(S,AR之间的转移关系已知),求解最优策略
Summary: 与环境交互产生数据——> 通过数据求解最佳策略 需要同时兼顾二者,提升数据效率和计算效率
2.1 马尔可夫决策过程
(1)马尔可夫过程MP
对于一个马尔可夫过程(一类随机过程),Xt+1的分布只和Xt的取值有关,和Xt之前发生过的事情无关。一环扣一环的因果关系,形成马尔可夫链。


马尔可夫链的核心性质:如果已知某些条件,要求解某些表达式关于这些条件的期望,则事实上只需要距离所求事件最接近的条件就足够了。
一个随机过程能不能用马氏过程来建模,在于能否很好地定义状态以及状态之间的转移方程。
(2)马尔可夫决策过程MDP
MP只有状态及状态间的内在关系,在MDP中,增加行为$A_t$与奖励$R_t$。
- 增加$A_t$相当于增加“主观能动性”,作为系统输入。
- 增加$R_t$相当于采取行动带来的回报,类似系统输出
使得MDP中状态间的转移关系不再是内部的,而是由状态St与行为At共同决定。

$R_t$由$s_t$和$a_t$共同决定,服从概率分布。
MDP中,核心目标就是求出一种选择$A_t$的方式,使获得的奖励最多。
结束信号 $Done_t$:代表MDP何时结束
(3)MP与MDP对比
马氏链和MDP,最重要的性质是它们各个变量之间的关系必须满足马尔可夫性。
- MP
-
给定条件概率$P(S_{t+1} S_t=s_t)$,以及初始状态分布$P(S_0)$,就完全确定了马氏链的分布 - 对于所有的s与t,可以求得所有$P(S_t=s)$
- 对于所有马氏链轨道$(s_0,s_1,…,s_n)$ ,可以求得其发生的概率$P(\tau=(s_0,s_1,…,s_n))$
-
- MDP
- 给定P、R、Done,以及初始状态分布$P(S_0)$,后续$S_t$的分布也无法确定。因为还存在可以自由选择的$A_t$
-
当$P(A_t S_t=s)$确定时,一切就确定了,可以求得$P(S_t=s)$、$P(A_t=a)$、$P(R_t=r)$的具体分布 - 并且对于可能发生的所有轨道$(s_0,s_1,…,s_n)$ ,可以求得其发生的概率$P(\tau=(s_0,s_1,…,s_n))$
Summary:
MP具有“客观规律”的系统,不受外部输入影响。MDP则不断接受外部输入($A_t$),研究MDP目的就在于选择最佳的行动。
2.2 MDP的分类
我们最终要求解的强化学习问题应该是一个环境未知且持续多步的MDP,这导致我们的算法要同时考虑两个方面的困难,即如何与环境交互产生数据、如何求解最佳策略。 在考虑MDP的基本性质之后,考虑MDP中状态转移方程是否具有随机性,以及是否具有时齐性,可以帮助我们确定我们需要的解(最优策略)是什么形式 MDP中动作与状态的连续性与随机性对于我们的算法也是很重要的,因为这决定了我们将会采用何种模型;此外,我们还可以考虑MDP是否能把时间也定义为连续的。
(1)MDP是否发生退化
有的强化学习问题,状态转系关系P发生了退化,可以理解为每一盘游戏只包含一个回合(区别于下象棋) Example:Multi-armed Bandit(多臂老虎机)、Contextual Bandit(上下文老虎机)
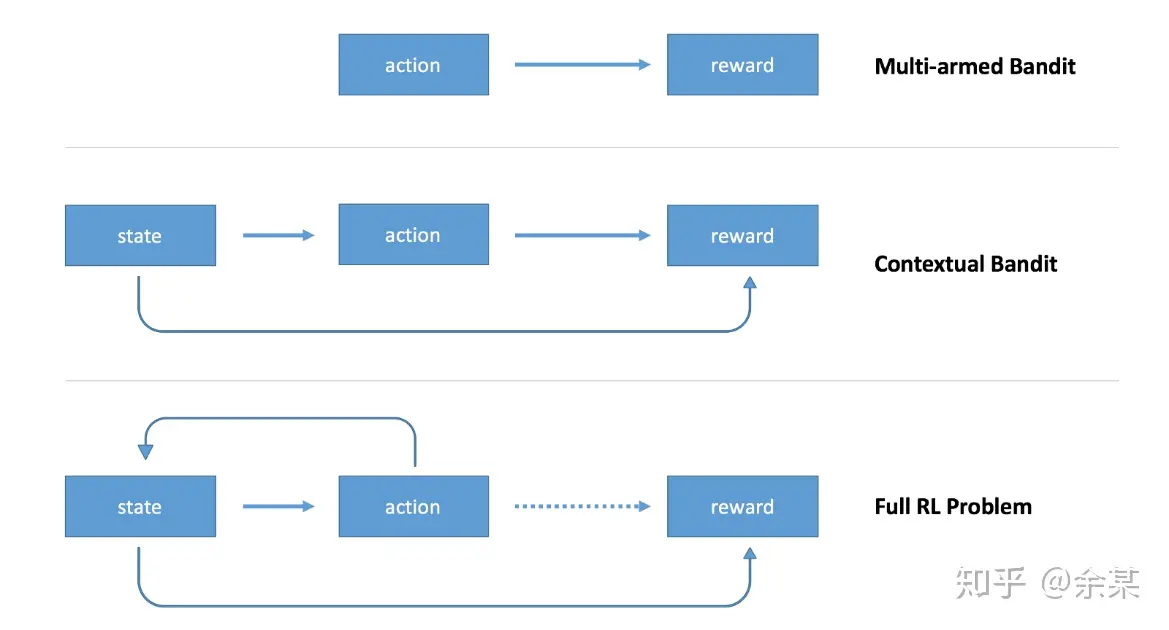
解决此类问题相比于一般的RL问题更简单,例如针对MAB,只需要与环境不断交互产生数据,估计出哪一个$a$对应的$R_a$的期望最大即可
(2)环境是否已知
完全已知的环境—最优控制:找到一种最优地控制智能体的策略,使其在环境中取得最小的损失(追求最大化效用)。前提是环境已知(转移概率P与奖励的概率模型R已知)
部分已知的环境—不知道P与R的表达式。先从现实中收集大量服从于P与R分布的数据,估计近似的$\hat{P}$与$\hat{R}$,然后再将其当作环境已知的MDP并利用最优控制的方法去求解它的最优解,将其近似为最佳策略
非常复杂的环境—强化学习:现实中,对于动作与状态是连续的问题,尤其是其转移关系高度非线性的问题(例如状态是图像),只能直接从未知的环境中交互地不断产生数据,并从中学习最优策略。
Notes: 如果算法中的某个时刻,我们将环境表达式视为已知的(无论是“真的知道”还是仅仅通过近似估计得到),并基于这个表达式求解最优策略,则这就应该被归入最优控制的范畴; 而如果我们始终将环境视为一个未知的客体,并源源不断地从它那里获取数据,修正我们的策略(在Model-Based算法中还包括对于环境表达式的估计),则这就应该被归入强化学习的范畴。
区别: 最优控制——以线性模型等传统方法解决相对简单的、环境表达式已知的MDP;习惯将目标设定为最小化损失。 强化学习——以神经网络等模型来解决比较复杂的、环境表达式未知的MDP;习惯将目标设定为最大化奖效用。
(3)环境的确定性与随机性
在环境转移关系与初始状态均确定的情况下,我们要执行的动作和状态无关。
在环境转移关系确定、初始状态随机的情况下,我们要执行的动作和初始状态有关,和中间的状态没有关系。
在环境转移关系随机的时候,我们需要根据中间状态来确定动作。
Conclusion: 最终的解的性质取决于环境的随机性(初始状态分布$P(S_0)$以及状态转移关系$P_{s,s’}^a$)。 当初始状态$S_0$具有随机性时,我们的动作要取决于初始状态的取值: 当状态转移关系$P_{s,s’}^a$是一个随机分布时,我们每一步都要依据当前的状态选择最佳动作。 所得到的策略是一个关于状态S条件分布$P(A_t|S_t=s)$
当环境是随机时,我们要根据当前状态来判断动作; 而当环境是确定的时候,我们则不必根据游戏中的状态取值来判断动作,而可以预先决定所有动作的取值。 一般而言,对于未知的环境,我们总会假定环境具有随机性,否则就可能会导致疏漏。
(4)环境的时齐性
时齐性用于衡量环境与奖励是否会随着时间而发生变化。非时齐性表示状态之间的转移概率会随着时间变化而变化。
强化学习中,一般默认环境是时齐的。
时齐MDP中的“时间”是一种“相对的”度量标尺,例如“一年”、“一个回合”; 非时齐MDP中的“时间”是“绝对的”历史度量,例如“公元2018年”或者“第100个回合”。
如果MDP是时齐的(即状态转移关系、奖励、结束信号都是时齐的),则我们的最佳策略($a^*=policy(s)$)不需要根据时间来判断动作;
而如果MDP不是时齐的(环境转移关系、奖励、结束信号中有一个不是时齐的),则我们的最佳策略($a^*=policy(s,t)$)需要根据时间决定采取的动作
在很多具体的任务中,我们会假定奖励$R$或$Done$是非时齐的,因为我们不但希望奖励多,也希望它来的早。我们或许会设定一个最大的时间(即使游戏本来不限制时间),也或许会定义$R_t$是随着时间指数衰减的(即使游戏规则只考虑得分总和),例如定义我们的目标为极大化$E(\sum_t\gamma^tR_t)$,其中$\gamma$是一个小于1的衰减因子。
(5)状态与动作的连续性
在强化学习中,可以根据状态与行动是连续变量还是分类变量来对MDP进行分类。(类似类别有限的分类模型和连续变量的回归模型的区别)
在工程控制、工业机器人等领域,有大量问题都可以转化为$S$连续、$A$有限或者是$S$连续、$A$连续的MDP问题。
$S$有限、$A$有限的情况相对较少,出现在规则简单的游戏中,如棋牌类或者电梯中简单的控制系统
$S$有限、$A$连续的MDP相对更少,一般的问题中总会假定$S$比$A$更加复杂。
Summary: 状态与动作的连续性与否会使MDP定义和算法模型有很大不同。 动作是类别变量与连续变量的区别,就像是分类问题与回归问题的区别,这将会直接决定我们能够采用什么模型。
(6)时间的连续性
部分任务如下象棋,由于本身是回合制的,时间天然就是离散变量而无法改为连续变量;
而对于无人驾驶等恩物,从本质上来说是时间连续的MDP。但为了方便求解,通常会对时间进行离散化处理。只要$\Delta t$足够小就不会有影响。
时间$t$的连续与离散会导致问题性质有很大的不同。尤其是当时间连续时,状态转移方程和奖励计算都应采用微分和积分的形式。
Summary

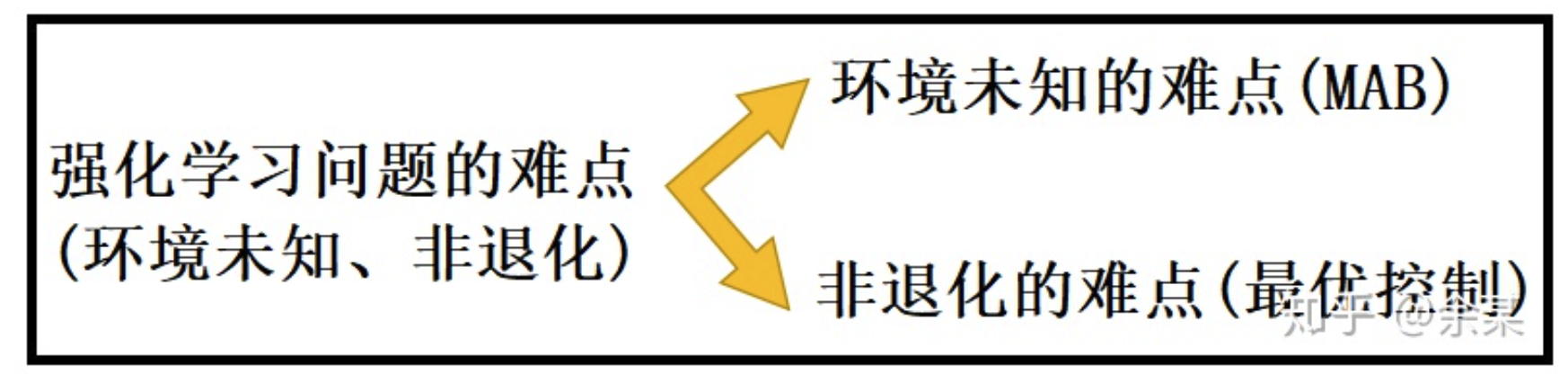
最重要、最值得关注的性质是MDP是否退化以及环境表达式是否已知。强化学习求解的是非退化且环境未知的MDP,故其难点主要来自两个相对独立的因素,一个是环境未知,一个是MDP持续多步。
3.1 多臂老虎机问题
多臂老虎机问题(Multi-Armed Bandit, MAB),即求解一个环境未知、退化的MDP。考虑这个问题实际上排除了求解最优策略的困难,而专注于环境未知的困难。
在环境未知的情况下,重要的是如何产生更有价值的数据,理解产生有价值的数据的方法。
(1)问题

该MAB是一个高度退化的强化学习问题,没有状态s,也不存在状态转移关系。但有5个不同的a可供选择。
由于MAB退化,故只需根据$R$而不用根据$V(s)$来确定最佳动作,求解最优策略。
但环境未知,只能通过产生数据去估计$R_i$。eg.对每个摇臂进行10次试验,得到奖励的平均值作为$\hat{E}(R_i)$。此时还剩下100次操作。
(2)法一

-
缺点:缺乏鲁棒性。估计得到的$\hat{E}(R_i)$并非真正的$E(R_i)$,进行多次试验后,各个摇臂的利润估计又会变化。
-
改进:应不断利用新产生的数据使估计越来越精确。改进后得到法二。
(3)法二

-
缺点:有一定鲁棒性,但较弱。解决了高估的问题,但没有解决低估的问题。
-
改进:任何时候都不能放弃“当前看起来较差的动作”,必须以一定的概率去选择此类动作。充分利用、充分探索,控制两者之间的比率。改进后得到法三。
(4)法三

- 缺点:
- 探索率的选择是由认为设定的,如何选择可能会影响结果。
- 用50次操作去得到初始化$\hat{E}(R_i)$。如何选择合适的初步探索的次数。
- 改进:初始化时,视作$\epsilon=1$即完全探索的过程。随着产生的数据增多,增加利用的比率,减小$\epsilon$。改进后得到法四。
(5)法四

小结:前期注重探索,后期注重利用。以何种规则减小$\epsilon$仍有可以改进的地方。
3.2 探索-利用困境(exploration-exploitation dilemma)
(1)基本思想
(2)常见的探索策略
4.1 价值的定义
4.2 动态规划
(4.3 LQR控制&4.4 H-J-B方程&4.5 变分原理)
5.1 Q值的思想
5.2 Q-learning
5.3 Sarsa
5.4 DQN
状态是连续变量,动作是有限变量的MDP(状态较为复杂,但可以进行的操作有限)