题目顺序来源https://programmercarl.com/
[toc]
1.数组
@20240605
1.1数组理论基础
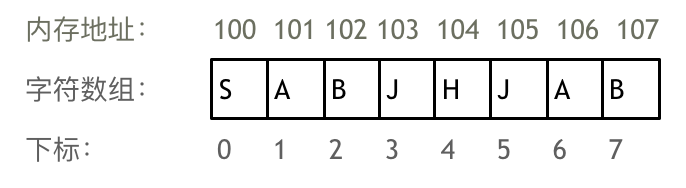
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
注意:
-
数组下标从0开始
-
数组内存空间的地址是连续的
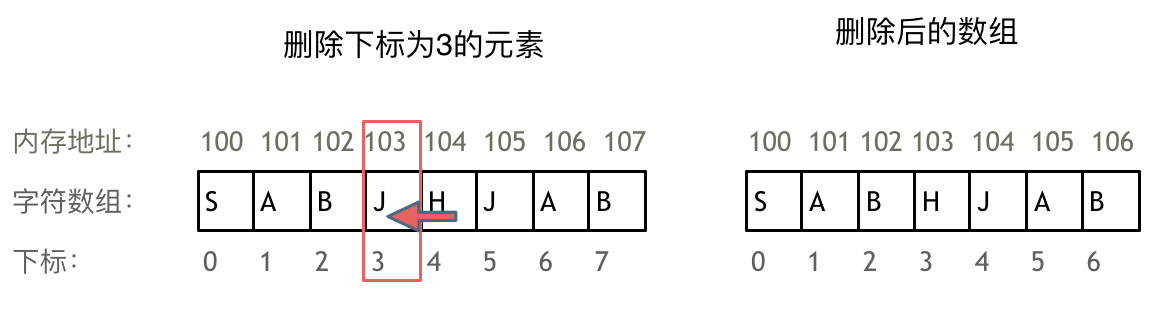
- 数组内存空间连续,增删元素时,其他元素地址也会随之变化
-
==数组元素不能删除,只能覆盖==,平时删除操作也是依次用后一位覆盖,因为申请初始化后,存储空间就固定了
-
二维数组在内存的空间地址是否连续?
Python中的常见序列有:字符串、列表、元组、字典、集合
其中:
- 列表:用于存储任意数目、任意类型的数据集合,是包含多个元素的有序连续的内存空间。包括append(x)、pop([index])、remove(x)、index(x)、count(x)、len(list)、reverse()、sort()、copy()
1.2二分查找
问题描述
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
#704.二分查找: https://leetcode.cn/problems/binary-search/description/
解决思路
题目中有两个重要信息,一是已知nums数组为升序数组(注意与非降序的区别),二是数组中不存在重复元素。
二分查找的核心思想主要在于不断缩小查找空间。
- 假设有两个指针
i、j,用于标记区间所在位置,初始化值为0,整个数组的长度-1。另有索引m,计算方式为(i+j)//2 - 比较
nums[m]和target的值,根据比较结果通过i,j修改区间范围,按照要求输出结果
Python代码——==双闭区间==
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def search(self, nums: List[int], target: int) -> int:
i = 0
j = len(nums) - 1
while i <= j:
m = (i + j)//2 # 可改进
if nums[m] < target:
i = m + 1
elif nums[m] > target:
j = m - 1
else:
return m
return -1
解析补充
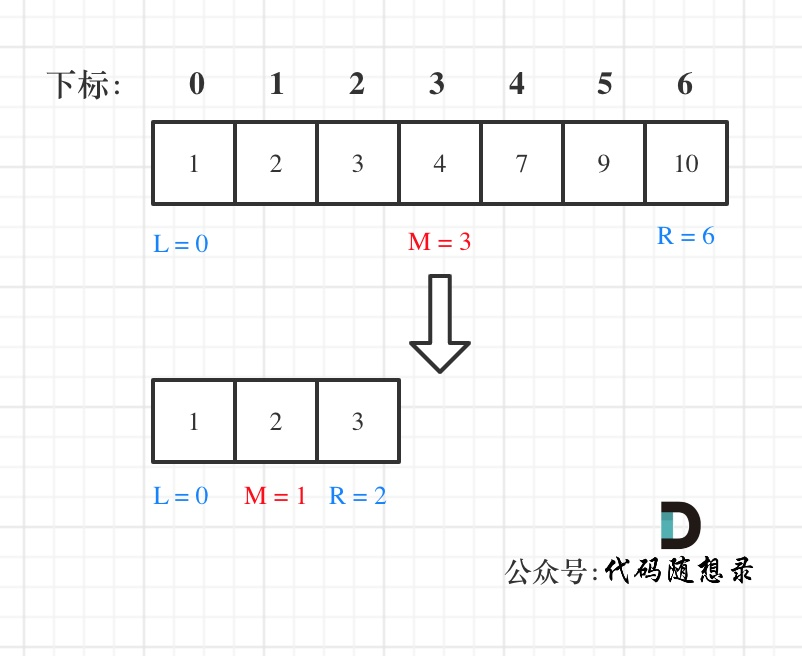
法一:我们定义 target 是在一个在左闭右闭的区间里,也就是[left, right] (这个很重要非常重要)。
区间的定义这就决定了二分法的代码应该如何写,因为定义target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]
while left <= right:
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle - 1 # target在左区间,所以[left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target在右区间,所以[middle + 1, right]
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
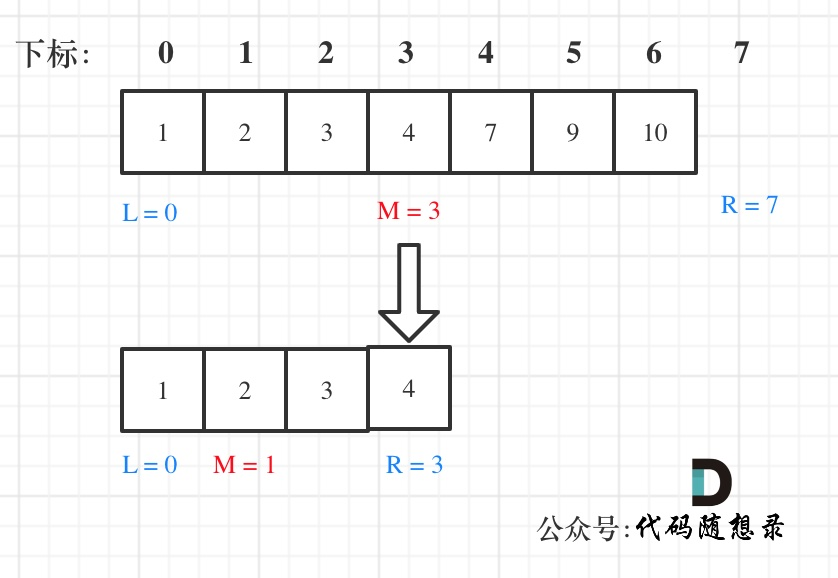
法二:如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
有如下两点:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) # 定义target在左闭右开的区间里,即:[left, right)
while left < right: # 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle # target 在左区间,在[left, middle)中
elif nums[middle] < target:
left = middle + 1 # target 在右区间,在[middle + 1, right)中
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
==总结说明==
值得注意的是,由于i和j都是 int 类型,因此i+j可能会超出 int 类型的取值范围。
为了避免大数越界,我们通常采用公式$𝑚=⌊𝑖+(𝑗−𝑖)/2⌋$来计算中点。
而非简单采用$m = (i + j)//2$。
@20240606
1.3移除元素
问题描述
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。 - 返回
k。
#27.移除元素:https://leetcode.cn/problems/remove-element/description/
解决思路
由于数据元素不能直接删除,只能覆盖。根据提示0 <= val <= 100,直接将数值等于val的元素赋值为101。再对nums进行排序、切片,返回所需结果。
Python代码
1
2
3
4
5
6
7
8
9
10
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
k = len(nums)-nums.count(val)
for i in range(len(nums)):
if nums[i] == val:
nums[i] = 101 # 直接根据定义范围用固定数覆盖,有待改进
nums.sort()
nums = nums[0:k]
return len(nums)
解析补充
法一:暴力解法。两层for循环,一个for循环遍历数组元素 ,第二个for循环更新数组。
删除过程如下:发现第一个需要删除的元素时,依次用后一个元素覆盖前一个元素,直到覆盖至最后第二个元素。
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
i, l = 0, len(nums)
while i < l:
if nums[i] == val: # 找到等于目标值的节点
for j in range(i+1, l): # 移除该元素,并将后面元素向前平移
nums[j - 1] = nums[j]
l -= 1
i -= 1
i += 1
return l
法二:双指针法(快慢指针法)。通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
定义快慢指针
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新新数组下标的位置
相当于边查找边覆盖。删除过程如下:发现第一个需要删除的元素时,快指针继续前往下一个元素,若不需要删除,则用该元素覆盖慢指针处的元素。随后,两指针继续寻找、更新。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
# 快慢指针
fast = 0 # 快指针
slow = 0 # 慢指针
size = len(nums)
while fast < size: # 不加等于是因为,a = size 时,nums[a] 会越界
# slow 用来收集不等于 val 的值,如果 fast 对应值不等于 val,则把它与 slow 替换
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
法三:相向双指针法。通过左、右指针来调整数组元素。
删除过程如下:
- 左指针指向的是无需删除的元素,左指针向右移动
- 右指针指向的是需要删除的元素,右指针向左移动
- 若有左指针指向删除元素,右指针指向无需删除的元素,则右指针的元素值赋给左指针的元素,且左右指针各自向右、向左移动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 相向双指针法
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
n = len(nums)
left, right = 0, n - 1
while left <= right:
while left <= right and nums[left] != val:
left += 1
while left <= right and nums[right] == val:
right -= 1
if left < right:
nums[left] = nums[right]
left += 1
right -= 1
return left
==总结说明==
在解决问题时,多尝试考虑指针的方法,应当尽量保证解决方案的可扩展性,而非一题一解。
@20240616
1.4有序数组的平方
问题描述
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
#977.有序数组的平方:https://leetcode.cn/problems/squares-of-a-sorted-array/description/
解决思路
逐步解决问题:
- 将原来数组中的元素更新为该元素的平方
- 以非递减顺序输出(借助sort()方法)
Python代码
1
2
3
4
5
6
7
class Solution: # 暴力排序
def sortedSquares(self, nums: List[int]) -> List[int]:
for i in range(len(nums)):
nums[i] = nums[i] ** 2 # nums[i] *= nums[i]
nums.sort()
return nums
解析补充
法一:(题目中的已知条件为原数组也是非递减顺序排序的。可以利用这一点采用双指针法。)
数组其实是有序的, 只不过负数平方之后可能成为最大数了。
-
那么数组平方的最大值就在数组的两端,不是最左边就是最右边,不可能是中间。
-
此时可以考虑双指针法了,i指向起始位置,j指向终止位置。
-
定义一个新数组result,和A数组一样的大小,让k指向result数组终止位置。
-
如果
A[i] * A[i] < A[j] * A[j]那么result[k--] = A[j] * A[j];。 -
如果
A[i] * A[i] >= A[j] * A[j]那么result[k--] = A[i] * A[i];。
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
l, r, i = 0, len(nums)-1, len(nums)-1
# float('inf')是单精度浮点数的最大值,正无穷,直接用res=[]则后面赋值时会越界
res = [float('inf')] * len(nums) # 需要提前定义列表,存放结果
while l <= r:
if nums[l] ** 2 < nums[r] ** 2: # 左右边界进行对比,找出最大值
res[i] = nums[r] ** 2
r -= 1 # 右指针往左移动
else:
res[i] = nums[l] ** 2
l += 1 # 左指针往右移动
i -= 1 # 存放结果的指针需要往前平移一位
return res
法二:暴力排序法+列表推导法
1
2
3
4
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
return sorted(x*x for x in nums)
==总结说明==
仔细观察思考已知条件。
@20240627
长度最小的子数组
问题描述
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的子数组[numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0` 。
#209.长度最小的子数组:https://leetcode.cn/problems/minimum-size-subarray-sum/description/
解决思路
一开始尝试暴力法,运行无误,提交时报错。
1
2
3
4
5
6
7
8
9
10
11
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
nums.sort()
ans = len(nums)
for i in range(len(nums)):
if sum(nums) < target:
return 0
n_num=nums[i:]
if sum(n_num) >= target and len(n_num) < ans:
ans = len(n_num)
return ans
发现没有仔细阅读题干,要求的是连续子数组,对原数组进行排序后,数组被打乱,导致错误。
借鉴了其他人的暴力法,尝试提交发现超时。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
l = len(nums)
min_len = float('inf')
for i in range(l):
cur_sum = 0
for j in range(i, l):
cur_sum += nums[j]
if cur_sum >= target:
min_len = min(min_len, j - i + 1)
break
return min_len if min_len != float('inf') else 0
改为使用滑窗法。
Python代码
1
解析补充
==总结说明==
@Date
Template
问题描述
#704.二分查找: https://leetcode.cn/problems/binary-search/description/
解决思路
Python代码
解析补充
==总结说明==