西湖大学 赵世钰老师
Ch0 Introduction
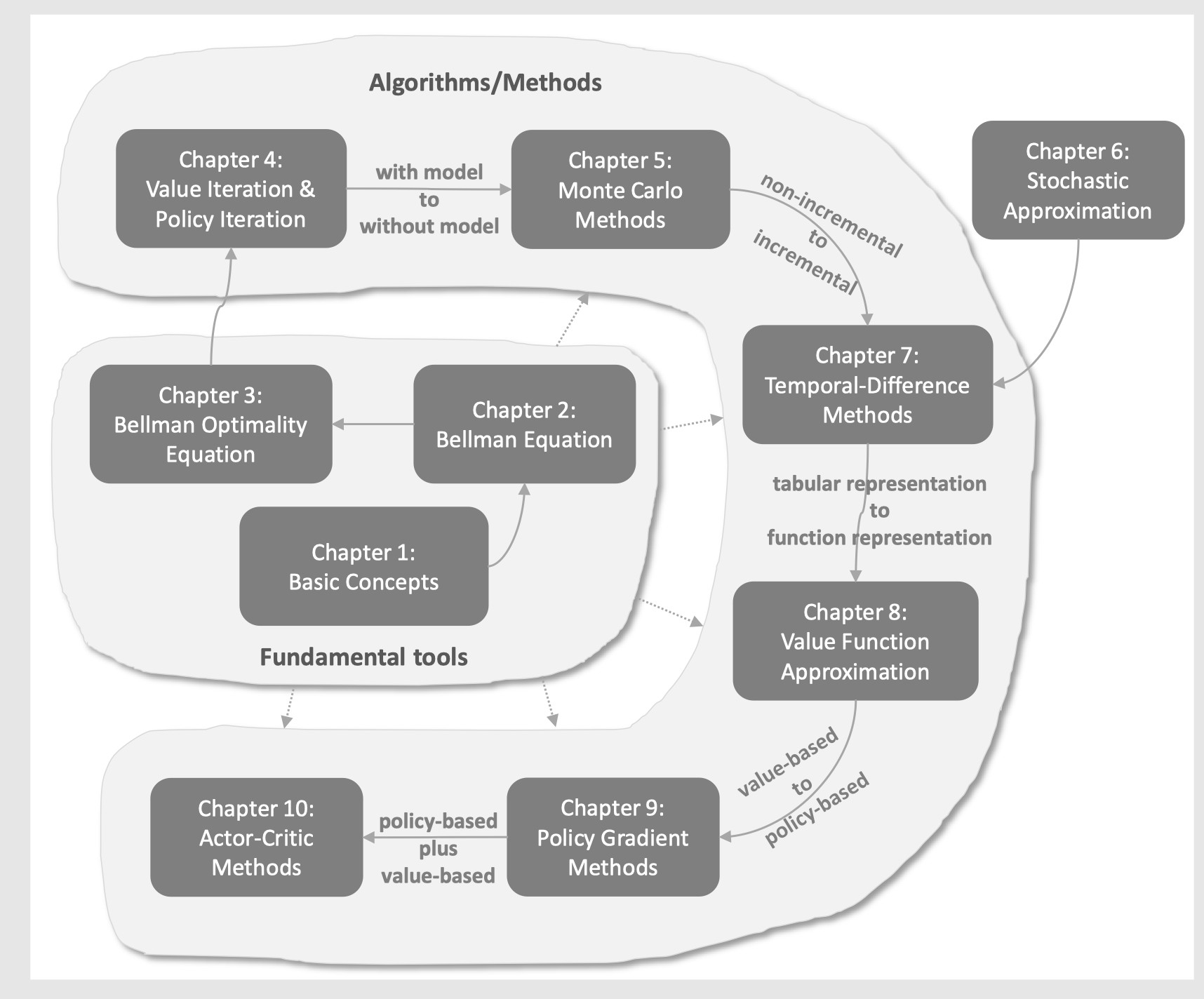
Ch1-3 基础概念、贝尔曼
Ch4-8 用不同的方式去计算value
Ch9 直接优化policy
Ch10 结合policy和value
Ch1 Basic Concepts in Reinforcement Learning
Markov Decision Process
- Markov:Markov property
- Decision Process:Policy
- Process:Use sets and probability distribution to describe it

Some key concepts:
- State
- Action
-
State transition, state transition p robability $p(s’ s,a)$ -
Reward, reward probability $p(r s,a)$ - Trajectory, episode, return, discounted return
- Markov decision process
Ch2 State Value and Bellman Equation
State value 和 action value都是为了能够评估、得到更好的policy

Ch3 Optimal policy and Bellman optimality equation
- 贝尔曼公式:给定策略
- 贝尔曼最优公式:求解策略 (是一个特殊的贝尔曼公式,其中采用的固定策略就是最有策略$\pi^*$)
在贝尔曼最优公式中,状态值($v(s)$、$v(s’)$)和策略($\pi(s)$)都是未知的,可以通过固定$v$的方式,迭代解得$\pi$。
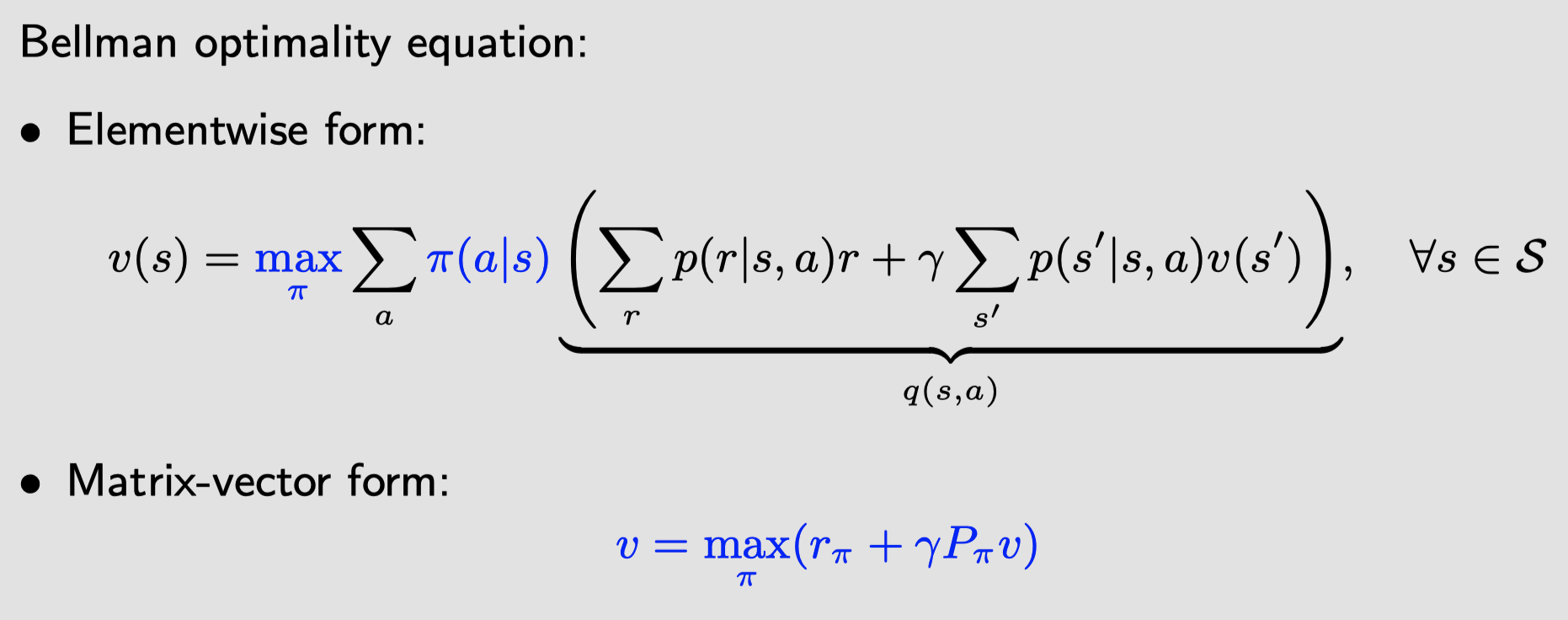
Optimal policy ==$\pi^*$==
| $\pi^*(s)=\arg\max_\pi\sum_a\pi(a | s)\underbrace{\left(\sum_rp(r | s,a)r+\gamma\sum_{s^\prime}p(s^\prime | s,a)v^(s^\prime)\right)}_{q^(s,a)}$ |

Conclusion
It is clear that the shorter the trajectory is, the greater the return is. Therefore, although the immediate reward of every step does not encourage the agent to approach the target as quickly as possible, the discount rate does encourage it to do so.
A ==misunderstanding== that beginners may have is that adding a negative reward (e.g., −1) on top of the rewards obtained for every movement is necessary to encourage the agent to reach the target as quickly as possible. This is a misunderstanding because adding the same reward on top of all rewards is an affine transformation, which preserves the optimal policy. Moreover, optimal policies do not take meaningless detours due to the discount rate, even though a detour may not receive any immediate negative rewards.

Ch4 Value Iteration and Policy Iteration
$v$和$\pi$区分:
- $v$—— state value
- $\pi$——policy
Policy iteration(start from $\pi_0$)
